Reply to TICS review

Commentary on Frisby et. al. (2023)

There was a nicely written review article published at the beginning of 2023 in Trends in Cognitive Sciences (link). It is clear much work went into the article, and I am a fan of the endeavor undertaken by the paper’s authors. However, while I think an important distinction between independent and conjoint codes is made throughout the paper, if my understanding is correct, I am also afraid that there might be a misrepresentation of this distinction throughout the paper. I’m writing this to make clear what I think the misunderstanding is and bring it to the attention of the authors.

Problem Statement

Frisby et. al. make a distinction between independent and conjoint codes and, while I agree this is a meaningful distinction, the paper appears to make several incorrect claims about how the presence of a conjoint code can be assessed. Throughout the paper, there is the repeated claim that analysis techniques that “depend on activation patterns across multiple units” are capable of detecting “conjoint” codes. Throughout the rest of this blog-post, I’ll illustrate that it is in fact only non-linear analysis techniques that are capable of detecting what the paper calls conjoint codes, and most commonly used multivariate pattern analysis (MVPA) techniques such as representational similarity analysis (RSA), and linear support vector machines (SVMs) are not sensitive to conjoint codes.

Background

First, we start with the definition the paper gives for the relevant terms. Quoting:

Conjoint

(of a representation) consisting of units that express different semantic information depending on the states of other units.

Independent

(of a representation) consisting of units that express the presence or absence of the same semantic information irrespective of the states of other units

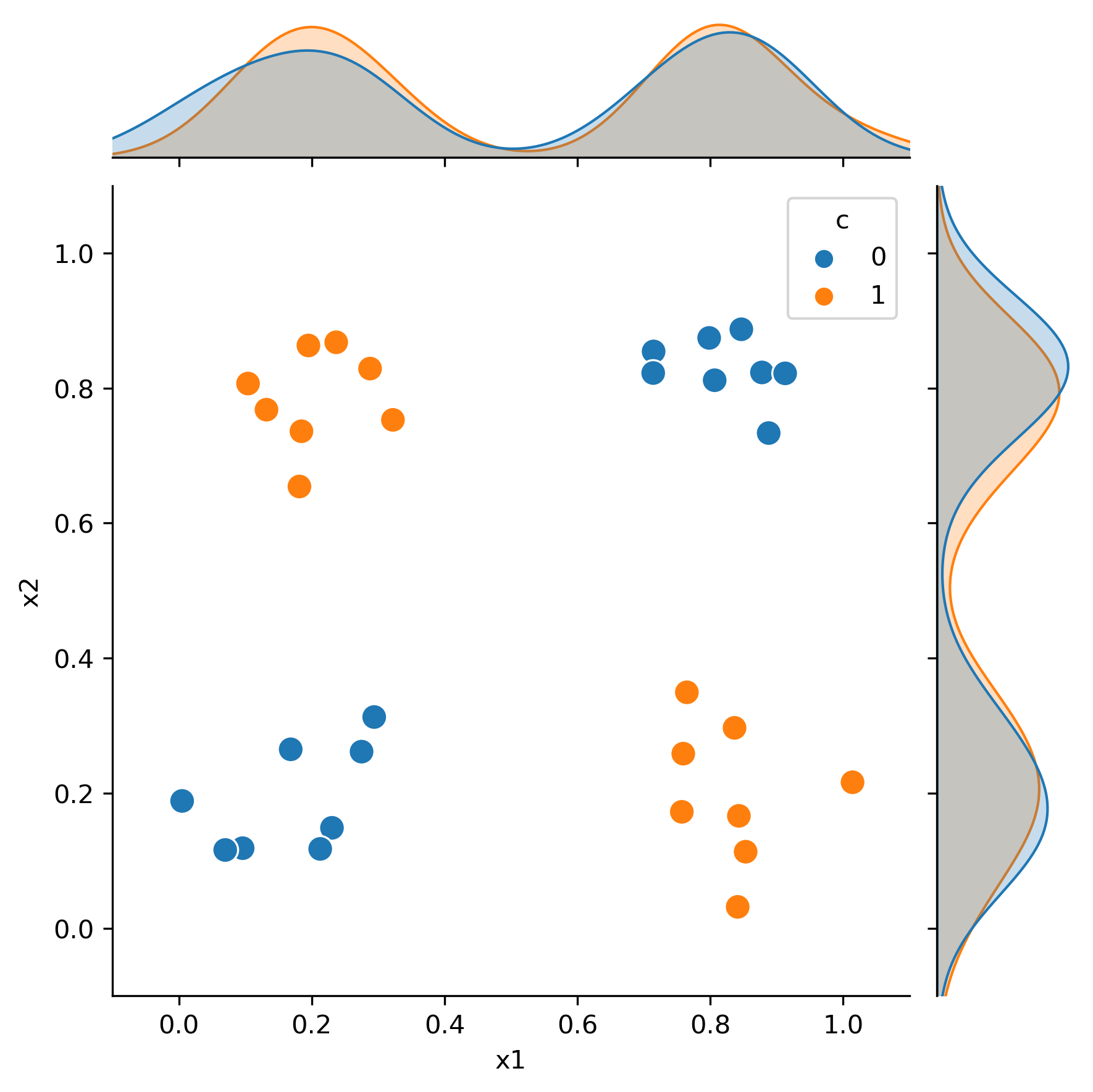
This distinction is made clear in Figure 2B in the paper using the canonical example of a conjoint code: the XOR problem. This problem is made famous by the fact that no linear network can decode the system and it is the classic motivating example for a multi-layer perceptronWhile a single layer perceptron cannot solve this problem, multi-layer perceptrons can. I’ve recreated the classic XOR problem here:

Click here to see data for plot

	c	x1	x2
0	0	0.230472	0.148776
1	0	0.0960016	0.118623
2	0	0.275045	0.261598
3	0	0.294056	0.312897
4	0	0.00489648	0.188605
5	0	0.069782	0.115984
6	0	0.212784	0.117552
7	0	0.168376	0.265059
8	0	0.79832	0.874325
9	0	0.714696	0.854315
10	0	0.88794	0.733449
11	0	0.877779	0.823216
12	0	0.806603	0.811669
13	0	0.912724	0.821869
14	0	0.846751	0.887143
15	0	0.714071	0.82236
16	1	0.236875	0.867891
17	1	0.104112	0.806758
18	1	0.287845	0.828912
19	1	0.195007	0.863129
20	1	0.181514	0.654284
21	1	0.131907	0.768033
22	1	0.322254	0.752963
23	1	0.184547	0.736112
24	1	0.757167	0.172486
25	1	0.764787	0.349494
26	1	0.853231	0.113417
27	1	0.836544	0.296828
28	1	0.841273	0.031713
29	1	0.843082	0.166511
30	1	1.01416	0.216275
31	1	0.759358	0.258622

This classification problem illustrates a case where only knowing one feature provides no information about the category membership of a datapoint (shown in the marginal distributions). However, knowing the value of both x1 and x2 it is easy to perfectly classify each data point.

What Frisby et. al. don’t draw attention to is that only non-linear systems can solve the XOR problem. It is not the case that multivariate methods are, in general, able to detect conjoint codes. Linear SVMs, RSA, and vertex-wise encoding models are all not sensitive to information represented in conjoint codes. On this account, the paper makes incorrect statements. Quoting:

Because neural similarities are computed across multiple units, the technique [RSA] can detect conjoint or independent codes.

Another example:

Because the output of a classifier depends on activation patterns across multiple units, MVPC can detect both independent and conjoint codes.

Again, only non-linear classifiers can detect conjoint codes.

[regularization] can detect conjoint representations (page 13)

The specific examples of L1 and L2 penalized regressors are most commonly used to regularize cases of multiple linear regression. Penalization does not change whether a given model is capable of detecting non-linear mappings between inputs and outputs.

Frisby and colleagues compiled a list of 100 papers that they go through to determine if a conjoint or independent code is assessed in each paper. Following what they lay out in the text, RSA is included in the conjoint category, but this is incorrect. To emphasize this, I demonstrate the failure of RSA and linear SVMs on the XOR problem.

RSA and XOR problem

The shown XOR problem has 32 datapoints that belong to two distinct classes. The task is to use the value of x1 and x2 to determine the class of the datapoint. As stated, the resultperhaps surprising is that no linear classifier can perform this task. This property is what Frisby et. al. refer to as independence, or that class identity can’t be decoded by looking at any single feature but can be decoded by looking at both simultaneously.

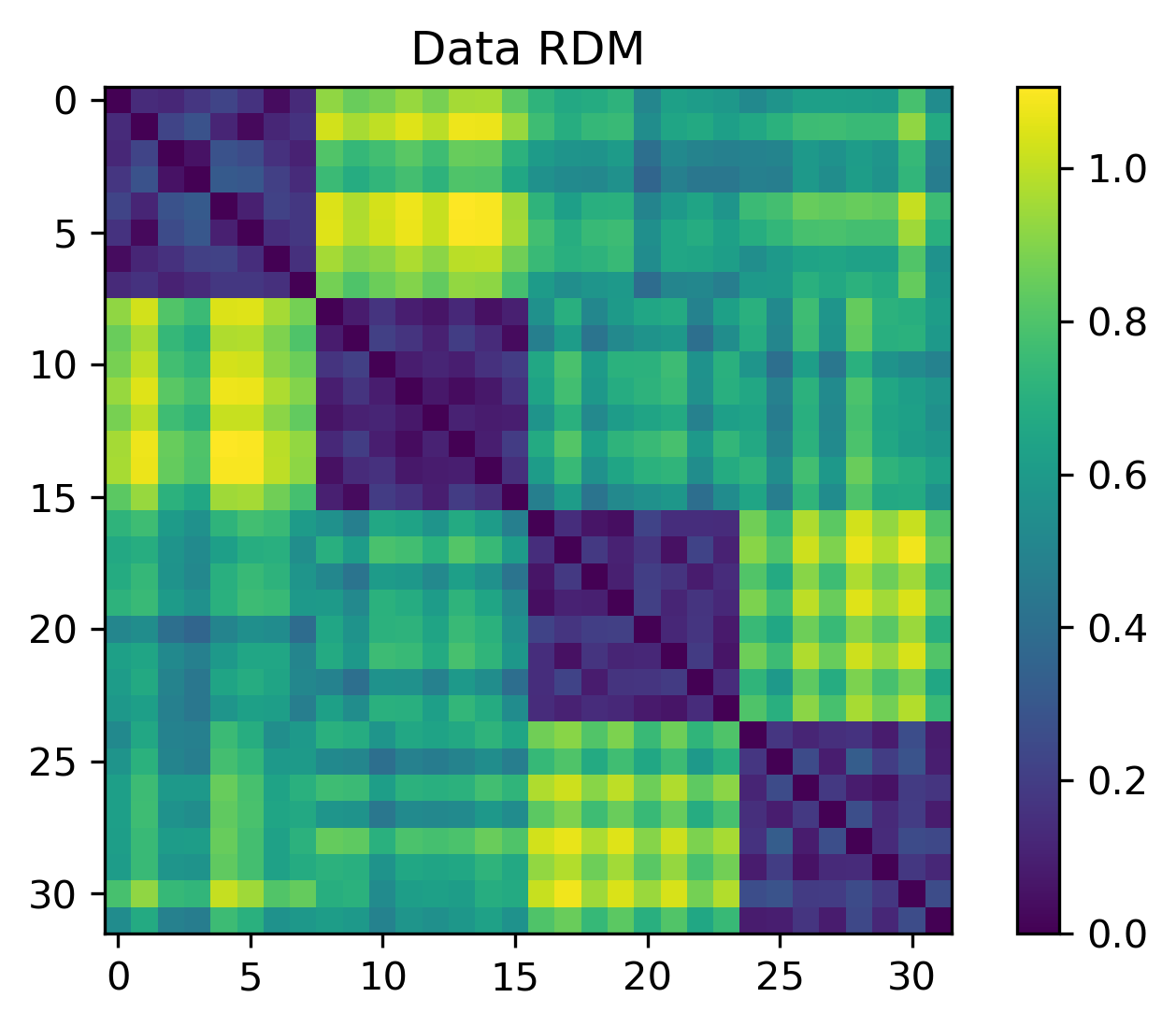
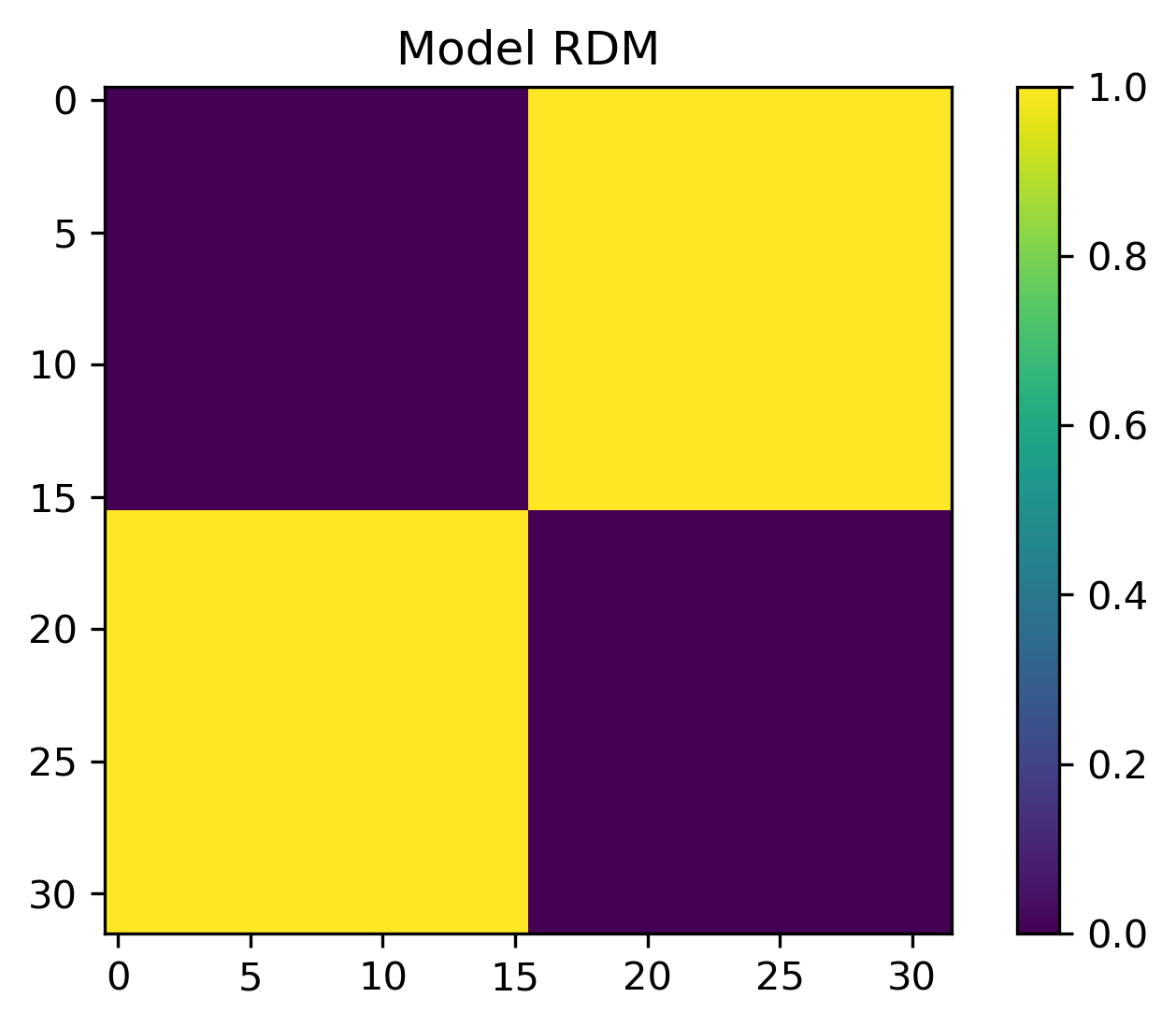
To show RSA fails to capture non-linear categorical structure, we can create an RDM from the data points and the target categories

Calculating the spearman correlation between the off-diagonal entries we get:

SignificanceResult(statistic=-0.001690, pvalue=0.97004) 

We see that for the canonical XOR example, RSA is insensitive to the conjoint code.

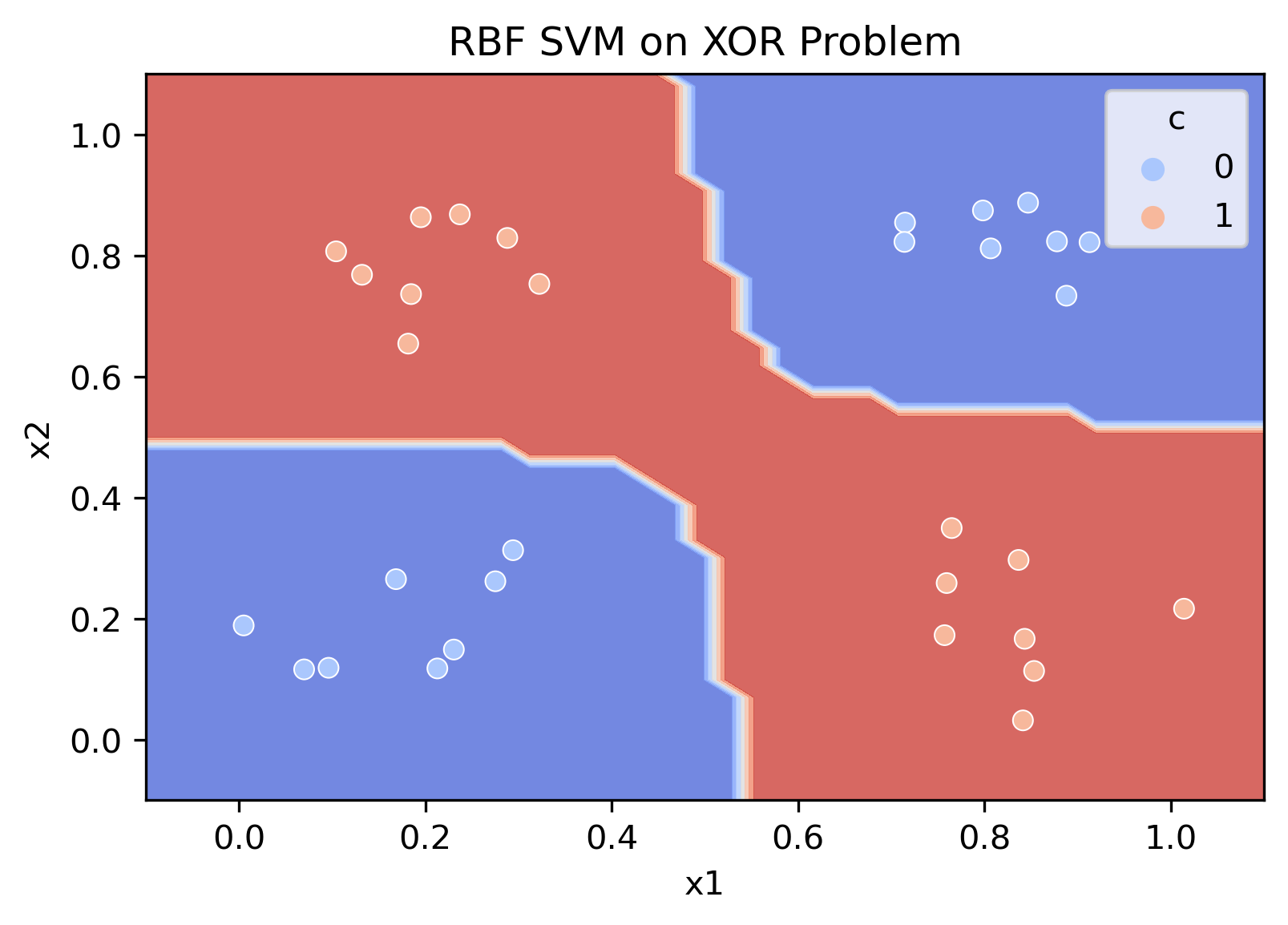
XOR and SVM

This section illustrates that linear support vector machines are also insensitive to the conjoint code

This section was generated using the python sklearn library with the following code (where df contains the values in the above table)

from sklearn.svm import SVC 
from sklearn.inspection import DecisionBoundaryDisplay 
mdl = SVC(kernel='linear').fit(df[['x1','x2']],df['c']) 
DecisionBoundaryDisplay.from_estimator(mdl,df[['x1','x2']],alpha=.8,cmap=plt.cm.coolwarm, 
response_method='predict') 
sns.scatterplot(data=df,x='x1',y='x2',hue='c',palette='coolwarm') 
plt.xlim([-.1,1.1]); plt.ylim([-.1,1.1]) 

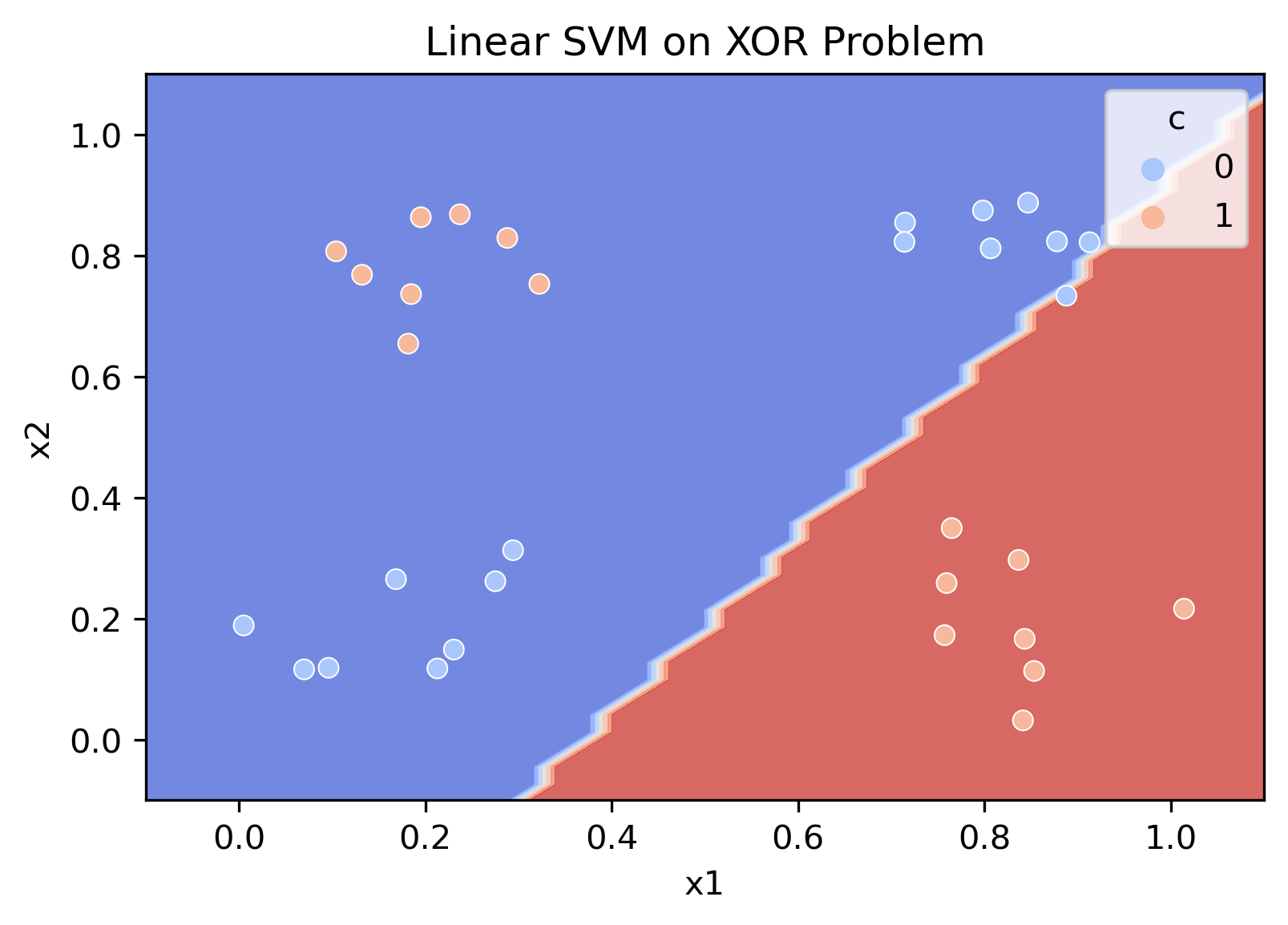
We can clearly see that linear boundaries cannot decode the conjoint code. However, once a non-linearity is introduced into the system, the classifier immediately decodes the joint code.

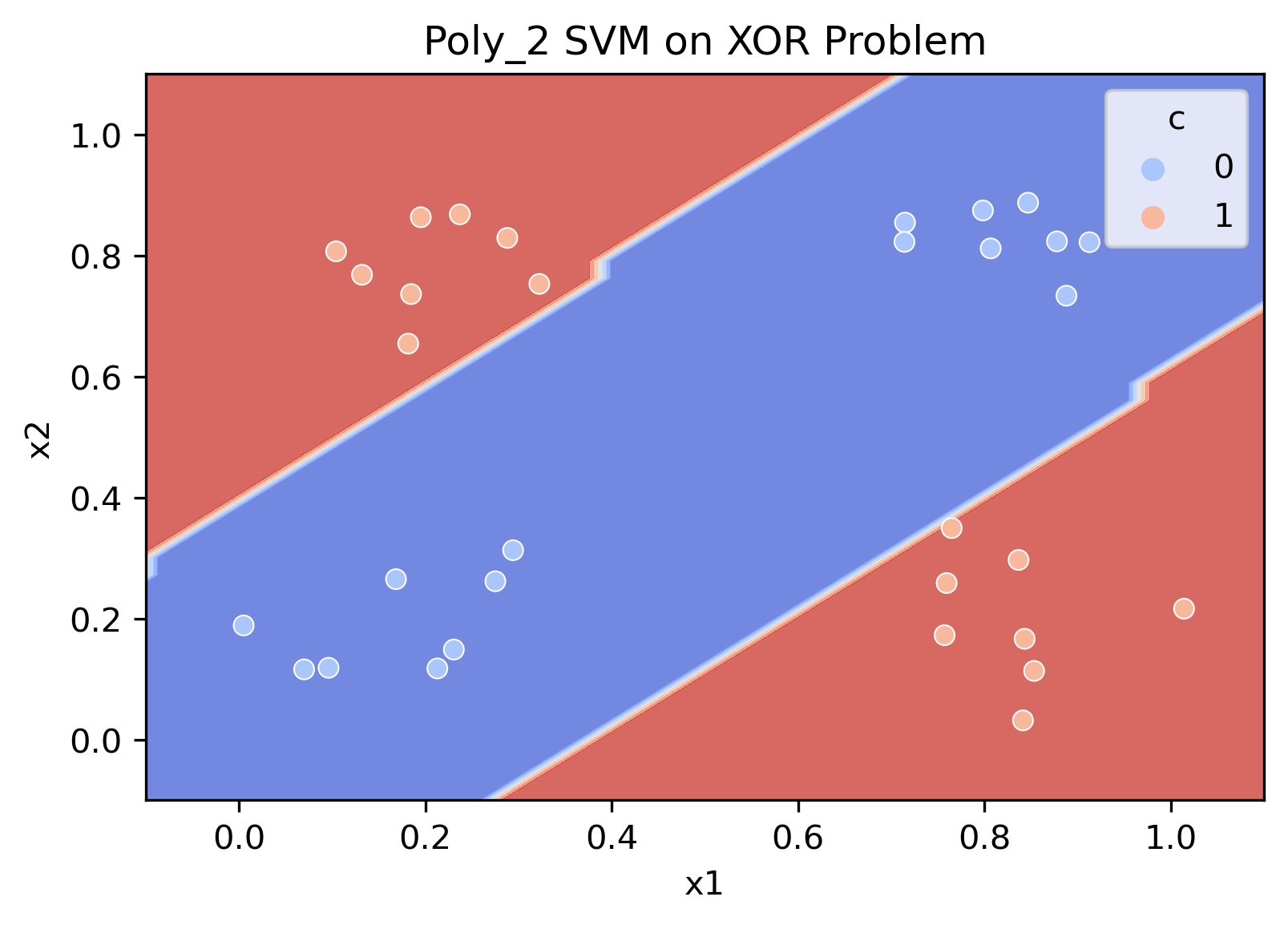
This last figure shows that even having a degree 2 polynomial basis function allows for solving the XOR problem.

Why it matters

Although it appears to me that conjoint and independent codes are misrepresented throughout the paper, I do want to emphasize that the paper points to an interesting distinction. That is, while RSA, linear SVMs, and (regularized) encoding models cannot detect conjoint codes, the question still stands about whether any type of information is conjointly encoded in the brain.

Properly understanding the relation between the multivariate methods is important so that researchers can build off of a common understanding. For me, one central paper that has shaped/formed my understanding is one by Jörn Diedrichsen and Nikolaus Kriegeskorte.

They show that RSA and linear vertex-wise encoding models are actually capturing the same information! If you’ll excuse the long quote, I think their conclusion captures the important takeaway.

The main purpose of this paper was to provide a clear definition of one important class of models —representational models— and to compare three important approaches of testing these. We have shown that PCM, RSA and encoding analysis are all closely related, testing hypotheses about the distribution of activity profiles. Moreover, all three approaches, in their dominant implementations, are sensitive only to distinctions between representations that are reflected in the second moment of the activity profiles. Thus, these three methods are properly understood as components of a single analytical framework.

Thanks for reading! Sincerely, I know that there is a far-from-zero likelihood that I’m misinterpreting some component(s) of the paper. Feel free to email me or comment with your thoughts!